Silk of the Sea

 This blog has lain dormant for some time, due mostly to my getting busy with repair/renovation projects around the house as well as to getting back into more active gaming, with two different online groups that I once played with in person.  I do mean to get back and finish out my sailing rules, and maybe revisit some of my earlier posts with tides, waves, etc to clean them up a little.  Ideally, I'd like to post a couple of seafaring type adventures where these rules come together in a way that matters, rather than just looking at them as curiosities.

But for now, I'm going to offer up a real-world luxury item that could be a fantasy world trade good.

https://www.atlasobscura.com/articles/sea-silk-rarest-thread-italy-clams-textiles-fabric

Sail Plans, Two Masted Vessels

The next set of sailing vessels, following logically from the single-masted vessels, will be those with two masts.  Just as a recap, there were some vessels touched on in the last post that could have more than one mast, the caravel and the lugger. Two masted versions will tend to be a little bigger, and will suffer a little from wind shadow (where the sails on the forward mast are at least partially blocked from the wind by the sails on the after mast) when sailing directly downwind. 

There was another type that I overlooked last time, or maybe I intentionally left it out and don't remember why; this one is the felucca.  Feluccas were lateen-rigged ships (a type of fore-and-aft rig originating in the eastern Mediterranean) with 1-3 masts. If I can find anything that sets lateen sails apart from any other fore-and-aft rigging scheme, I'll get around to developing those details into game mechanics, but for now, feluccas will probably be grouped in with another type of vessel for game purposes.

• Brig 

  

  Refundpolitics, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons

A brig's main allotment of sails includes square sails on both masts, but also a fore-and-aft gaff sail on the mainmast (situated to the rear with a foremast in front) and headsails.  Their heavy use of square sails gives them speed at sea, where winds are generally strong and blow steadily from one direction, but the fore-and-aft sail and headsails offer maneuverability and better handling along coasts where winds can be light and variable.  Brigs can be quite large and tend to require larger crews to handle all these sails.

• Yawl 

  

  By Casito at the English-language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2543192

A yawl has most of its sail area on the mainmast, with a much smaller sail on its mizzen mast, situated far to back of the ship, generally behind the rudder post.  All sails are fore-and-aft. Yawls are easily handled by smaller crews.

• Ketch 

  

  By Casito at the English-language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2543154

A ketch is very similar to a yawl, with fore-and-aft sails on a large mainmast and a much smaller mizzen.  The mizzen mast of a ketch is before the rudder post (not as far back as a yawl's).  As a war vessel, ketches are usually equipped with a mortar on the deck ahead of the mainmast, and used to bombard shore installations.  Such a vessel is referred to as a bomb ketch.

• Brigantine 

Refundpolitics, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons

The brigantine is similar to the brig, with square sails on the foremast, and a gaff-rigged mainsail with at least one square-rigged topsail above it on the mainmast.  (The difference is that the brig has a square mainsail with a small gaff sail right behind it, and a brigantine has a gaff mainsail with no square sail in that position.)  Brigantines are relatively fast and maneuverable, making them a good all-around rig, equally suited to coastal work and the open sea.

• Hermaphrodite Brig 

By Casito - https://en.wikipedia.org/w/index.php?title=File:Sail_plan_brigantine.svg, CC BY-SA 1.0, https://commons.wikimedia.org/w/index.php?curid=22001195

Similar to the brig and brigantine, the hermaphrodite brig or schooner brig has a square-rigged foremast and and fore-and-aft rigged mainmast, without square topsails.  

• Schooner 

By Casito at the English-language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2543169

Schooners have two or more masts, all rigged fore-and-aft.  They're common vessels for coastal trading.  The rig can be handled with a small crew (important for commercial shipping, and also because winds just off shore can be highly variable, requiring frequent adjustment), and is handy sailing upwind.

• Topsail Schooner 

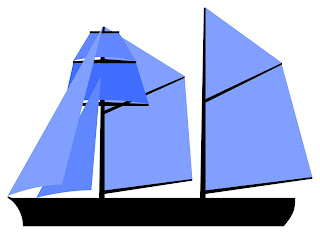KDS444, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons

As a schooner, but with square topsails situated above the fore-and-aft sails on one or more masts.  The square topsails require more crew to set, but provide better speed in steady, more-or-less downwind directions than fore-and-aft sails alone.

Sail Plans, Single Masted Vessels

    Different types of sailing vessels have different arrangements of sails, giving each one different advantages and disadvantages in ship handling.  The most basic distinction to be made is whether the sails on a given mast are square-rigged (hung more or less perpendicular to the length of the hull) or fore-and-aft (hung parallel to the length of the hull).  Generally speaking, square-rigged sails allow faster speed when sailing downwind, while fore-and-aft sails allow better sailing into the wind and are a little easier to adjust to changing conditions (whether the wind changes direction often or the ship is changing its orientation with regard to a wind blowing steadily from the same direction).

    There's only so much that can be done with one mast, so this particular post will be pretty short.  As I've mentioned before, my personal inclination is to use vessels from more modern periods in my games, sort of anachronistically.  But, rather than just limiting this series of occasional posts, I'm going to open it up to earlier times periods as well.  Therefore, the vessels I will talk about today will be (in rough chronological order) cogs, caravels, sloops, cutters, and luggers.

• Cog

By I, VollwertBIT, CC BY-SA 2.5, https://commons.wikimedia.org/w/index.php?curid=87406684

        Cogs were developed in the early medieval period, putting them squarely in the standard D&D time frame.  Single-masted and square-rigged, they weren't very agile, but their flat bottoms made them useful for trade in those early days when ports were pure luxuries.  Just run it up on a shallow beach and you're good to go.  The standard D&D "small sailing ship" is almost certainly meant to be a cog.

• Caravel

By Retábulo de Santa Auta - Museu de Arte Antiga, Lisbon, Portugal, Public Domain, https://commons.wikimedia.org/w/index.php?curid=23280190
This caravel has two masts, but you get the idea.

        Caravels generally had 2-4 masts, but the earliest ones sometimes had just one, so I'm including them here.  Caravels could have square-rigs or fore-and-aft rigs, and all had shallow keels that allowed them to run in shallow waters along shore or up rivers.  They made their first appearance in the early Renaissance era, and were of great importance in the early Age of Discovery.

• Sloop

        Sloop is weird kind of term, meaning different things at different times, and typically including a variety of types (technically cutters and luggers are types of sloops, but I'm keeping them separate, at least for now; also, at one point in time, the British navy considered anything not worth shooting at by a line-of-battle ship to be a sloop).  For our purposes, a sloop is a single-masted, fore-and-aft rigged vessel with a single headsail (the triangular sail in front of the mast).  A sloop without the headsail is a catboat (and I guess it's probably slower and less handy sailing to windward).  

By Kevin Murray - self-made SVG, based on w:en:File:Sloop_Example_Other.jpg by Kevin Murray, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2655573

        A sloop's mainsail can also be a gaff type sail.  Gaff sails have more sail area than the triangular Bermuda sails shown above, but aren't as handy sailing to windward.

By Casito at the English-language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2543178

        Technically a sloop can also have other sails.  I don't know if this monster is representative of anything that was actually built or if it's a hypothetical, but even if every one of these sails doesn't make its way onto a sloop, they are options.

By A loose necktie - Own work, CC0, https://commons.wikimedia.org/w/index.php?curid=98506347
Sloop sail plan showing crossjack, swallow-footed square-rigged topsail, save-all sail, topgallant sail, ringtail sail, gaff topsail, mainsail, and watersail, as well as foresail, jib, and flying jib

• Cutter

        Now's a good time to cut away to a vignette.

Together they stood on the jetty and watched the slow-moving vessel tacking towards her anchorage. She was some seventy feet in length, with a massive beam of over twenty. Single-masted, and with a rounded, blunt bow, she looked cumbersome and heavy, but Bolitho knew from what he had seen elsewhere that properly handled cutters could use their great sail area to tack within five points of the wind and in most weathers. She carried a vast, loose-footed mainsail, and also a squared topsail. A jib and fore completed her display of canvas, although Bolitho knew she could set more, even studding sails if required.

Midshipman Bolitho and the Avenger, Chapter 2, Alexander Kent

        A cutter is a type of sloop with multiple headsails.  They often have outsized bowsprits to support these headsails.  A naval cutter, like the one in the vignette here, carries square-rigged topsails, giving it downwind speed, while its headsails and gaff sail give it good handling to windward.  The studding sails mentioned here are extra square sails hung from extensions on the yards.  They're for added downwind speed.  You don't want them up when you're sailing across the wind because they cause the vessel to heel over more while making it more likely that heeling will cause the sails and rigging to dip into the water, a good way to damage the ship, reduce speed, and slew it around onto the wrong heading all at once.

By KDS444 - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=33382230

By Casito at the English-language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2543139

By KDS4444 - Own work, CC0, https://commons.wikimedia.org/w/index.php?curid=51633414

• Lugger

By Suzanne Maltais - Own work, CC BY-SA 2.5, https://commons.wikimedia.org/w/index.php?curid=1393065

        Here's another type of vessel that can be single-masted or can have multiple masts.  The distinguishing characteristic of a lugger is that it carries lugsails, which kind of look like gaff sails, but have some minor distinctions.  If you read a fair amount of maritime fiction, you see a lot of references to luggers, but they're rarely important to the story; luggers tend to be fishing vessels or coastal traders and apparently just aren't swashbuckling enough to enter into the story.  To be fair, though, according to Wikipedia at least, luggers were popular with smugglers, for pretty much the same reason they were popular with fishermen and merchants: they handle well to windward.  This is much more important along a coast, where the wind might change fairly frequently and where you might reasonably expect to sleep in your own bed (or at least in a nice dry bed on shore) at the end of your working day.  Square rigged vessels are more suitable for ocean crossings where the wind blows more steadily from one direction.

Right, anyway, I need to hammer out in-game distinctions for some of these concepts.  Pointing them out and listing them will help to systematize it all, instead of just letting random possible ideas bouncing around my skull until the end of time.  Maybe next time I'll have rules worked out, or maybe I'll just list some two-masted vessel types.  Either way will be progress, I suppose.

Things to work out:  Square-rig sailing speed downwind, fore-and-aft points of sail into the wind, shallower/deeper drafts, gaff rigs, catboats/under-sailed rigs, "extra" sails/stud sails, lugsails

Letterlocking

 In the olden days, before primeval office supply stores began selling envelopes, when paper was too rare and precious to waste on such things as envelopes, people kept their letters from being read by couriers (either specifically hired as such, or the travelers who casually filled in as couriers in what passed for a postal system at the time) by an intricate series of folds, often quite difficult to replicate, called letterlocking.

(Atlas Obscura has a few articles about letterlocking:

https://www.atlasobscura.com/articles/what-did-people-do-before-envelopes-letterlocking

https://www.atlasobscura.com/articles/letterlocking-virtual-unfolding

https://www.atlasobscura.com/articles/letterlocking-how-to )

I see two ways right off the bat of using these in-game:

    1) The PCs intercept a message between enemies of theirs and want to know what it says, but also don't want the enemies to know they know.  How can they tease this letter apart and get it back together without the final recipient realizing that it's been compromised?  (Magic probably, although it can be done without, and whichever method is used, getting there should be interesting.)

    2) Gamemasters who like making props can have a quest-giver or other major NPC send the PCs a message with an interesting letterlock applied.  For a further twist, perhaps a particular friendly NPC can be known to the PCs as always using an unusual letterlocking method; later, they intercept a message to an enemy of theirs with the same letterlock on it.  (The third link above has three letterlocking methods you can use.  It may be worth experimenting with some origami animals or paper fortune teller type things as well.)

Vignettes of the Sea, part 2

 I've been reading through my collection of sailing-ships fiction, and finding that a lot of it doesn't give much detail on the topic I'm most interested in at the moment (that being ship handling: arranging the sails, coordinating the sails and the rudder to maneuver, etc).  Plenty of combat, a good amount of chain-of-command politics and the friendships or simple sense of duty between people risking their lives far from home, but not enough of the mechanical descriptions I want to get a good feel for sailing the ship itself.  I want a set of rules that take into account the restrictions of relying on the wind to move and don't just feel like driving a car around.  The Lord Ramage novels are a major exception, so I'll be posting a lot from them as I go.

Also, all this reading was starting to feel more like procrastination and less like research, so I went looking for the file I was sure I had started back before I took a break from blogging, with the intent to post a little about hull variations or sail plans or something, but I'll be damned if I've found it yet.  I may have to start all over on that; luckily rebuilding something you've already learned a fair bit about is at least somewhat easier than learning it in the first place.

Anyway, here's a piece from Ramage, where Lieutenant Ramage has been sent to take the crew off of a frigate that had stove in its side on a rock in an inlet off the Italian coast.  After driving off some French soldiers who had taken part of the ship and rescuing the British crew, Ramage needs to get his vessel turned around and headed back out the way he came in.

As she lay alongside the frigate, the Kathleen's bowsprit pointed at an angle towards the cliffs on which the Belette's bow rested, and Ramage saw the only way to sail out was to let the wind swing the cutter's bow round while her stern was held against the frigate. That would take her clear of the rocks at the foot of the next headland.

“Evans,” he called to the Bosun's Mate, “cut away the for'ard four lines, but hold on to the aftermost two. Pay out and snub if need be, but keep our stern in. Quartermaster, put the helm down.”

By now the jib had been sheeted in aback so that the canvas was as flat as a board. The wind began to push the cutter's bow round to seaward, but her long, narrow keel diverted some of the effort into a fore-and-aft movement so the Kathleen began to move astern.

Ramage glanced aft; the frigate's stern gallery, looking very battered from the Kathleen's earlier assault, was drawing level with the cutter's transom. Evans was directing seamen and alternately paying out the grapnel lines to allow for the movement astern, and then snubbing them, to keep the cutter's stern against the frigate and help lever the bow around.

Ramage watched until the Kathleen's stern was well clear of the outlying rocks ahead. The foresail had by now been hoisted and, like the jib, sheeted aback.

“Mr. Southwick, I'll have jib and foresail sheeted home, if you please.”

As soon as they started drawing, the Kathleen's sternway would be checked and she would start moving ahead but, without the mainsail drawing, would still pay off to leeward.

“Quartermaster, tiller amidships.”

A sudden crackling of muskets made him glance up at the cliff: a group of French soldiers were kneeling, muskets at their shoulders. Almost at once the Marines along the Kathleen's bulwarks fired back and the French promptly ducked.

The Kathleen heeled slightly as the wind filled the headsails, and gradually started gathering headway.

“Evans, cut away those lines! Quartermaster, meet her! Mr. Southwick, aft the mainsheet!”

Ten minutes later the Kathleen was broad-reaching along the coast heading for Bastia, and Ramage handed over the conn to Southwick while he went over to Captain Laidman who had, he realized, been tactfully keeping himself to the lee side of the quarterdeck.

• Ramage, Chapter 20

Vignettes of the Sea

 I've been reading some inspirational literature while I kick around ideas about how to handle, well, ship handling.  I've been keeping track of some particularly interesting passages as inspiration not just for particular rules, but for rulings in general.  Specifically, I've been keeping track of passages about tricky maneuvering, the effects of damage, and storms (and how they cause that damage).  The process of blowing ships apart with artillery is interesting and all, but I think most people have a pretty good handle on how that works.  If you have any doubts, go watch some Age of Sail type movies.

Anyway, here's a pretty cool bit from the first Lord Ramage novel by Dudley Pope, unsurprisingly titled Ramage.  Ramage is the third lieutenant of the British Royal Navy frigate Sibella when they encounter a French ship-of-the-line.  He awakens from a concussion to discover he's the highest ranking surviving officer, and has to figure out how to keep his wounded men alive with no surgeon and his unwounded men alive and uncaptured by the French, and, oh yeah, the Sibella is about to lose a mast, has no rudder, and will sink in spite of anything that can be done about it now, which incidentally, makes the loss of the ship his responsibility.  This vignette shows that part of his plan playing out, specifically using a fallen mast to slow the ship and slew it around, and timing the whole thing so the French ship can't just put a broadside into the Sibella and sink it right away.

He put the speaking-trumpet to his lips again and bellowed across the water at the French ship:

“Bon soir, messieurs!”

With the mouthpiece to his ear he heard, after what seemed an age, a puzzled “Comment?” being shouted back from the Barras's quarterdeck. He could imagine their astonishment at being wished good evening. Well, keep the initiative.

“Ho detto 'Buona sera.'”

He almost laughed at the thought of the expressions on the Frenchmen's faces as they heard themselves being told in Italian that they had just been wished “Good evening.” There was an appreciable pause before the voice repeated:

“Comment?”

By now the Barras was not more than fifty yards away: the bow wave was sharply defined and he could pick out the delicate tracery of her rigging against the night sky, whereas a few moments ago it had been an indistinct blur.

This is the moment: once again he lifted the speaking-trumpet to his lips. Now, he thought, let us commend ourselves unto the XVth Article of War and still take as long as we can about it, and he yelled in English:

“Mister Frenchman – the ship is sinking.”

The same voice answered: “Vot say you?”

“I said, 'The ship is sinking.'”

He sensed Jackson anxiously shifting from one foot to another. There was a strange hush in the Sibella and he realized the wounded were not making a sound. The Sibella was a phantom ship, sailing along with no one at the helm, and manned by tense and silent men.

Then through the speaking-trumpet he heard someone say in French, “It's a trick.” It was the voice of a man who held authority and who'd reached a difficult decision. He guessed the next thing he'd hear would be that voice giving the order to open fire.

“You surrender?” came back the question, in English this time.

Hurriedly Ramage turned his head towards the Bosun and called softly:

“Bosun – start chopping.”

He had to avoid a direct reply; if he surrendered the ship and then escaped, the Admiralty would be just as angry as the French at a breach of the accepted code.

Putting the speaking-trumpet back to his lips he shouted:

“Surrender? Who? Our wheel is destroyed – we cannot steer – we have many wounded...”

He heard the thud of the axes and hoped the noise would not travel across to the Barras: he must drown it with his own voice, or at least distract the Frenchmen's attention.

“– We cannot steer and we have most of our men killed or wounded – we are sinking fast – we've lost our captain –”

Damn, he couldn't think of anything else to say. Jackson suddenly whispered, “Livestock's killed, guns dismounted, burgoo's spoiled...”

“Yes, Mister,” Ramage yelled, “all our pigs and the cow have been killed – all the guns are dismounted --”

“Comment?”

“Pigs – you've killed our pigs!”

“Je ne comprend pas! You surrender?”

“You've killed our pigs--”

The devil take it, would that foremast never go by the board?

“– The cow has been dismounted – the guns don't give any more milk – the pig's making water at the rate of a foot every fifteen minutes!”

He heard Jackson chuckling and at that moment there was a crackling from forward and a whiplash noise as several ropes parted under strain. Then there was a fearful groan, like a giant in pain, and against the night sky he could see the foremast beginning to topple. It went slowly at first; then crashed over the side, taking the yards with it.

“Wilson! The topsail and spanker!”

He saw the spanker being sheeted home in the boom end as the topsail was let fall from the yard. A few moments later, when he looked back at the Barras, she had vanished: He realized the Sibella was swinging round to larboard faster than he expected, and he glanced aft. The Barras had been caught unawares – she was still sailing on her original course and had gone too far for her guns to be able to rake the Sibella's completely unprotected stern.

    -- Ramage, Chapter 2

Easing into Degenesis

     Last post I said I would come up with a some short descriptions of the different factions (called Cults) in Degenesis to make it easier for players to build a character without having to read hundreds of pages of lore, using the system hidden inside the old World of Darkness.  First, a short sentence or two description of each faction, then a short paragraph, then the multi-page description for those players who are really interested in that faction based on the previous descriptions.

    At first, I was thinking I'd have to write the short sentence and the short paragraph, but it turns out Degenesis already has a short paragraph on each Cult, and I had just forgotten that they existed after reading another 300 pages past that point.  A glossary helps though, so I made up at least the start of one (I'm sure I missed something somewhere). 

By the way, the edition I'm using was downloaded in April 2020.  The edition currently available is in one combined volume, so I don't know how my page numbers will match up, but hopefully it will help to get you started if you choose to look into this game. 

So, without further ado:

Spitalians – Healers, doctors, medical researchers; the front line against the Sepsis and the Psychonaut threat to Europe

Chroniclers – Information dealers and hackers; they pay for technological relics, with the end goal of setting up a new Stream (global information network)

Hellvetics – The most advanced military force in Europe, armed with triple-barreled assault rifles and full-body armor; often hired out as mercenaries

Judges – Bringers of law and order to northern Europe, by might of their hammers and flintlocks

Scrappers – Recoverers of the past; whether they work alone or as part of a team, Scrappers know where to find relics and technology from before the apocalypse and how to put it to use

Clanners – A catch-all term for any number of relatively small groups; Clanners can be stone-age hunter-gatherers or motorized nomads, but in any case, their Clan is their family

Anubians – African mystics with seemingly magical power over the Psychovores as well as cultural power over other Africans

Scourgers – African warrior caste armed with assault rifles and armor from before the apocalypse, and traditions extending much further back than that

Neolibyans – Followers of a creed first espoused by “the Libyan”, Neolibyans seek economic and political power through exploration, diplomacy, and trade

Apocalyptics – Dealers in all sorts of vice and crime: gambling, drugs, prostitution, human trafficking, piracy, and more

Jehammedans – A new Abrahamic religion, devoted to raising sheep and waging war; their destiny within the Cult is determined at birth

Anabaptists – A religious Cult devoted to wiping out the evils of the Psychonauts and making the Earth into a Paradise once more

Palers – The guardians of the Dispensers, servants of the Sleepers, heirs of the Recombination Group, phantoms in the night

Short paragraphs: pp 50-53 of Degenesis: Primal Punk (Book 1)

Main descriptions: all from Degenesis: Primal Punk (Book 1)

Spitalians: pp 150-163

Chroniclers: pp 164-177

Hellvetics: pp 178-191

Judges: pp 192-205

Clanners: pp 206-219

Scrappers: pp 220-233

Neolibyans: pp 234-247

Scourgers: pp 248-261

Anubians: pp 262-275

Jehammedans: pp 276-289

Apocalyptics: pp 290-303

Anabaptists: pp 304-317

Palers: pp 318-331

Character creation rules: all from Degenesis: Katharsys (Book 2)

Spitalians: pp 46-49

Chroniclers: pp 50-53

Hellvetics: pp 54-57

Judges: pp 58-61

Clanners: pp 62-65

Scrappers: pp 66-69

Neolibyans: pp 70-73

Scourgers: pp 74-77

Anubians: pp 78-81

Jehammedans: pp 82-85

Apocalyptics: pp 86-89

Anabaptists: pp 90-93

Palers: pp 94-97

GLOSSARY

 Aberrant – another name for Psychonaut

Alcove – a small Chronicler enclave

Ambrosia – a nanite fluid that gives Marauders their power

AMSUMO – a security robot; most have been infected by a virus and have corrupted programming

Ascetic – the laboring caste of the Anabaptist cult

Bedain – formerly known as Sicily; now a staging area for African forays into Europe.

Biokinetic – a Psychonaut with the power to reshape its body; generally found in Pollen and associated with Pandora crater.

Burn – a drug found in spore fields, trafficked by Apocalyptics; use of it contaminates the body with Sepsis

Bygone – people, technology, or times from before the Eshaton

Chakra – an early Hindu concept concerning energy centers in the human body; the Chakras seem to correspond to the Earth Chakras and the different Raptures

Cluster – a large Chronicler enclave

Codex – the system of laws enforced by the Judges, as set down by the First Judge and amended ever since by the High Judges

Corpse – the landmass formerly consisting of Sardinia and Corsica; now a stronghold of Apocalyptic pirates

Cusp – a papery growth found in spore fields containing Burn

Demiurge – in the Anabaptist tradition, the enemy of God and source of all evil

Dinar – the major currency of Africa; a gold coin

Discordance – a zone between the Earth Chakras of Europe and the Psychovore forests of Africa; the Primer creates strange, ethereal, membranous creatures here

Dispenser – cryogenic sleep chambers set up by the Recombination Group; Sleepers are supposed to emerge every hundred years from the Dispensers, although something seems to have gone wrong with the plan

Draft – the major currency of Europe; fiat currency issued by Chroniclers and pegged to the Dinar

Druschinnik – bodyguard of the Piast of Wroclaw (Pollen)

Dushani – Psychonaut with a sound-based powers that exert wave forces and manipulate minds; associated with the Balkhan and Usud crater

Earth Chakra – craters from the asteroid bombardment of the Eshaton; so called because they seem to correspond to the Chrakras of the human body from ancient Hindu beliefs

Elysian oil – oils made by the Anabaptists which enhance various mental or emotional faculties

Enigmate – Pregnoctic prophets who aid the Hybrispanians against the African conquerors

Eshaton – the apocalypse; caused by asteroids containing an alien mutagen 500 years ago

Famulancer – low level Spitalians, just beginning their study of medicine

Filament – a sharp force-field generated by Psychokinetics

Fractal Forest – strange forests that spring up from dead spore fields; revered by Anabaptists, distrusted by Spitalians, burned by Apocalyptics

Garganti – a Clan whose lifestyle is based around mammoths, which were genetically re-engineered before the Eshaton

Gendo – a wolf-like predator

Guardian – the technicians maintaining the Dispensers; Palers and their ancestors

Guerrero – a Hybrispanian Clan fighting against African conquerors

HIVE – Human ImmunoVirus Extreme; an airborne version of HIV

Iconide – Jehammedan mystic and maker of holy icons

Imiut skin – the skin of a jackal or Gendo, which an Anubian can sew a recently dead body into to return it to life

Janite – foreign mercenary soldier of Osman (Borca)

Kom – battle buggies used by Scourgers

Leperos – a person afflicted with Sepsis beyond help or hope; usually a Burn addict

Marauder – a creature (person?) of godlike power, powered by Ambrosia

Marduk oil – oil created by the Anubians; a layer of it on the skin blocks the effects of a Pheromancer's power

Mirar – the Earth Chakra of Hybrispania; associated with Pregnoctics

Mnemonid – a type of Pregnoctic

Mollusk – a biological device created by the Spitalians to detect Sepsis

Node – a powerful type of Pregnoctic

Nox – the Earth Chakra of Purgare; associated with Psychokinetics

Orgiastic – the warrior caste of the Anabaptist cult

Pandora – the Earth Chakra of Pollen; associated with Biokinetics

Pheromancer – a Psychonaut with pheromone based mind control powers; generally found in Franka and associated with Souffrance crater

Piast – the leader of Wroclaw (Pollen)

Pregnoctic – a Psychonaut with time based powers; generally found in Hybrispania and associated with Mirar crater

Preservist – a member of the security branch of the Spitalians

Primer – the name given to the alien mutagen which has given rise to the Earth Chakras, Psychovores, and Discordance

Protectorate – the area governed by the Codex of the Judges; capital: Justitian; stretches across parts of Borca and Franka

Psychokinetic – a Psychonaut with telekinetic and force-field type powers; generally found in Purgare and associated with Nox crater

Psychonaut – descended from humans, but no longer human, Psychonauts have strange powers that threaten humanity as we know it

Psychovore – Primer-altered plants from Africa; their thorns cause Raze

Rapture – any of the five main categories of Psychonaut powers

Raze – a type of poisoning from Psychovore thorns that inevitably leads to death if left untreated; Anubians are resistant to the Raze

Reaper's Blow – a long scar across Europe left by an asteroid strike; a region of magma flows, only crossable at certain points

Recombination Group – a Bygone cult based on memetic manipulation; built the Dispensers and the psychological environment of the Guardians just before the Eshaton so high-ranking members would be kept alive cryogenically and reborn into a world ripe for their takeover

Sepsis – contamination by the Primer

Shutter – a Chronicler assassin

Sleeper – Recombination Group cult members who were supposed to be released from cryogenic sleep in waves to take positions of power in the post-Eshaton world

Souffrance – the Earth Chakra of Franka; associated with Pheromancers

Soulless One – a Psychonaut

Spital – the headquarters of the Spitalians

Spitfire – a flamethrower used by the Anabaptists

Splayer – a spear-like weapon with scissoring blades used by the Spitalians

Stream – pre-Eshaton information network

Sun Disk – electronic tools that can be used to control technology and systems within the Dispensers

Usud – the Earth Chakra of Balkhan; associated with Dushani

Voivodate – a part of Balkhan ruled by a voivod (warlord)

Voivodule – a member of a Balkhan Clan of old (supplanted) nobility

Warpage – an area of Hybrispania where time doesn't work right as a side effect of the Pregnoctics and Mirar crater

Warui – a side effect of the Psychovores that creates a natural understanding to those affected; they can express complex thoughts with very few sounds, regardless of whether they share a common language